The Importance of Step Size in Optimizing Stochastic Gradient Descent Algorithm

The step size, also known as the learning rate, is a critical factor in optimizing the efficiency of the stochastic gradient descent (SGD) algorithm. Various strategies have emerged recently to enhance the performance of SGD by adjusting the step size. However, one significant challenge that arises with these strategies is the probability distribution of the step sizes assigned to different iterations.

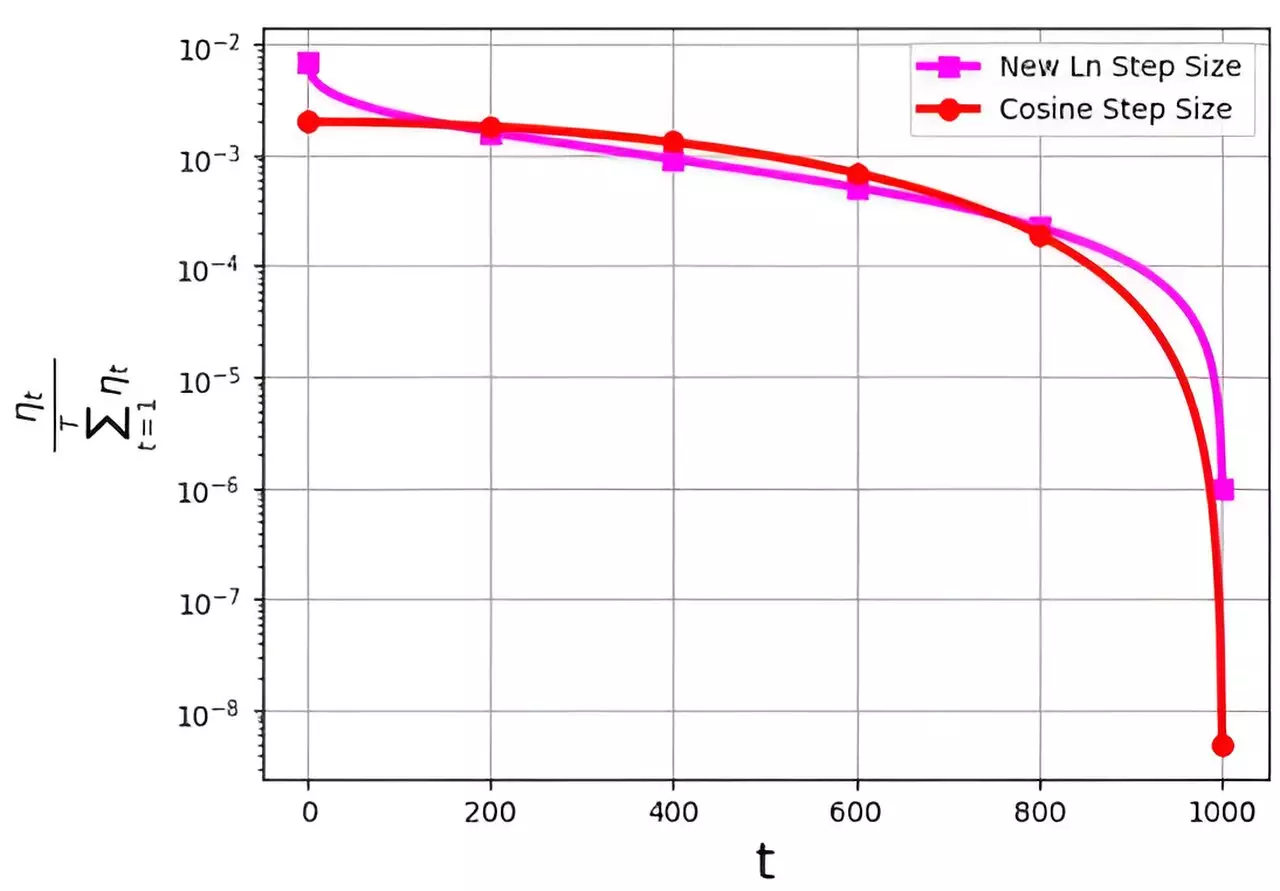
The probability distribution, denoted as ηt/ΣTt=1ηt, is crucial in determining the effectiveness of the step size strategy. It has been observed that some commonly used step size methods, such as the cosine step size, tend to assign very low probability distribution values to the final iterations. This poses a challenge as excessively small values may hinder the convergence of the algorithm.

In an effort to address this challenge, a research team led by M. Soheil Shamaee conducted a study that was published in Frontiers of Computer Science. They introduced a new logarithmic step size method for the SGD approach, which proved to be highly effective especially during the final iterations. The new step size method demonstrated a significantly higher probability of selection in the concluding iterations compared to the conventional cosine step size.

The numerical results obtained from the study served as evidence of the efficiency of the newly proposed logarithmic step size method. The research team tested the method on the FashionMinst, CIFAR10, and CIFAR100 datasets, showing remarkable improvements in test accuracy. For instance, when used with a convolutional neural network (CNN) model, the new step size method achieved a 0.9% increase in test accuracy for the CIFAR100 dataset.

The choice of step size in the stochastic gradient descent algorithm can significantly impact its performance. The research by M. Soheil Shamaee and team sheds light on the importance of selecting an appropriate step size strategy with a favorable probability distribution. The introduction of a new logarithmic step size method has shown promising results in enhancing the efficiency and accuracy of the SGD algorithm, particularly in the critical concluding iterations. Further research and experimentation in this area could lead to even more significant improvements in optimization algorithms.